TG1 基础数据结构

约定：本文的下标从1开始，代码尽量从1开始（我在努力习惯），一般使用$\LaTeX$美化

这一节主要介绍了一些基础的数据结构 （废话），前缀和，差分，二分查找，离散化，ST表，线段树等。

来给大家一一介绍一下

前缀和

求解问题:

给你一个数组$a$，$n$次询问，每次输入$l,r$,求$\sum\limits_{i=l}^ra[i]$ (就是a[l…r]的和)。

基本思想:

计算数组$b$，对于每一个$b[i]$,值就是$\sum\limits_{j=1}^ia[j]$.
对于每次的l,r询问，答案就是$b[r]-b[l-1]$.

 问题来了：如何快速计算$b?$

for(int i = 1;i <= n;i++)
	b[i] = a[i] + b[i-1];

 我们只需要将前缀和累加即可。

 如果我们不需要原来的$a$了，这样写代码可以减少内存的浪费 （别和我扯空间复杂度）,
$\ \ \ \text{\color{red}注意,a[0]一定要=0！}$

for(int i = 1;i <= n;i++)
	a[i] += a[i-1];

差分

求解问题:

 给定一个数组$a$，$n$次操作,每次给定$l,r,v$,使区间a[l,r]都加上v.输出最后的数组

差分其实就是前缀和的逆运算（可以这样理解），计算差分和计算前缀和一样简单：

$\\ \color{red}{\text{注意，像有损前缀和一样的，for语句要倒着写！}}\\ \color{black} \text{为啥呢？请看下面这个：}\\ a={1,9,2,6,1,8,1,7}\\ \text{我们手玩是这样的（也就是无损的）} b={1,8,-7,4,-5,7,-7,6}\\ \text{但是如果正着减的话，就会变成这样：}\\ a={1,8,-6,12,-12,20,-19,26}\\$

1. 无损
    

for(int i = 1;i <= n;i++)
	b[i] = a[i] - a[i-1];

2. 有损
    

for(int i = n;i;i--)
	b[i] -= b[i - 1];

二分查找

求解问题

求函数零点。

实现

upper_bound和lower_bound

非常的简单

离散化

求解问题

 当数很大的时候，我们往往不能直接拿来存数组，这就是离散化的思想了。

实现

三部曲

1. sort
2. unique
3. lower_bound 或者 upper_bound

例题：

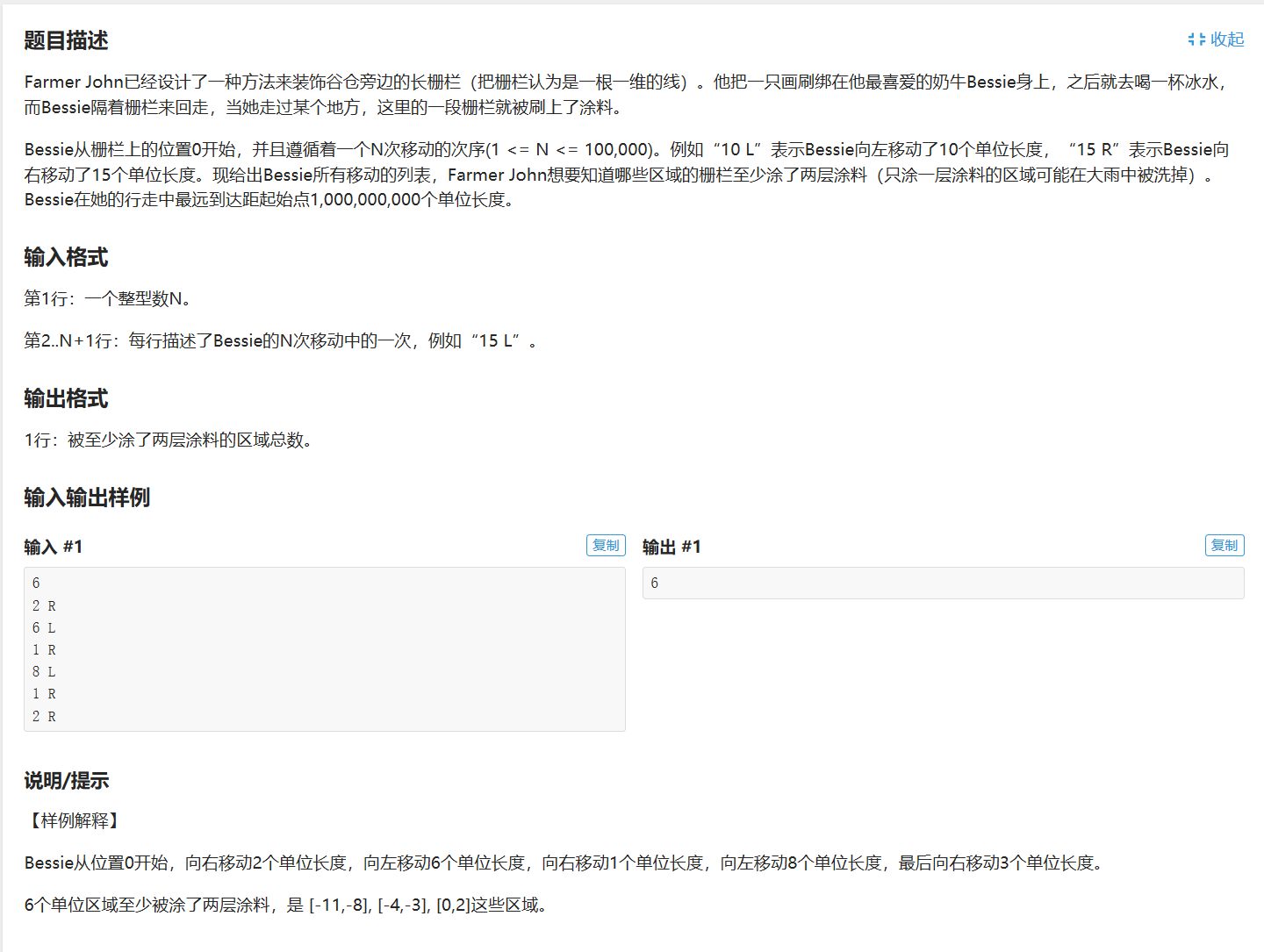
其实道理是非常简单的，唯一的问题就是数据范围非常的大，导致无法直接计算。怎么办？
这时就可以运用离散化的思想了。

但是，当我们再细细看题的时候： Bessie在她的行走中最远到达距起始点1,000,000,000个单位长度。
我的天！！！这个天才Bessie走这么远，我们要是乖乖开数组的话空间会不够的！！！这时我们又可以从什么方向入手呢？
我们回到我们一开始进行模拟的步骤，如果我们进行以下的移动的话会很简单： 3 R 2 L 3 R

0	1	2	3	4
1	2	2	2	1

（第一行是位置，第二行是经过次数）但如果变成这样会很麻烦： 1000000 R 500000 L 1000000 R
More Actions。。。这个要是要写表格的话会死人的吧；但是这简单来写的话是不是这样呢？

。。。这个要是要写表格的话会死人的吧；但是这简单来写的话是不是这样呢？	0	1	2	3	4	5	6	7	8	9
	1	1	3	3	3	3	1	1	0	0

要是再简单点呢?	0	1	2	3
	1	3	3	1

出处

为了锻炼读者的代码阅读能力 （懒）,这个代码不添加任何注释。

#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
const int maxn =  2000010;
int a[maxn],b[maxn],c[maxn],n,sum,ans;
int o;char p;
void Paint(int ll,int rr)
{
	int l = lower_bound(b,b+n+1,ll)-b;
	int r = lower_bound(b,b+n+1,rr)-b;
	if(l>r)swap(l,r);
	c[l]++;c[r]--;
}
int main(void)
{
	scanf("%d",&n);
	for(int i = 1;i <= n;i++)
	{
		cin>>a[i]>>p;
		if(p == 'L')a[i]=-a[i];
		b[i] = b[i-1] + a[i];
	}
	sort(b,b+n+1);
	int m = unique(b,b+n+1) - b;
	for(int i = 1;i <= n;i++)
	{
		Paint(sum,sum+a[i]);
		sum+=a[i];
	}
	sum = c[0];
	for(int i = 1;i<m;i++)
	{
		if(sum > 1)ans+=b[i]-b[i-1];
		sum+=c[i];
	}
	cout<<ans<<endl;
}

总结

离散化，说白了，就是把大数化小数的过程。

树状数组

先看一道题:

$\mathrm{Quz1:何为树状数组}$？

就是没有右儿子的线段树。

处理的问题：

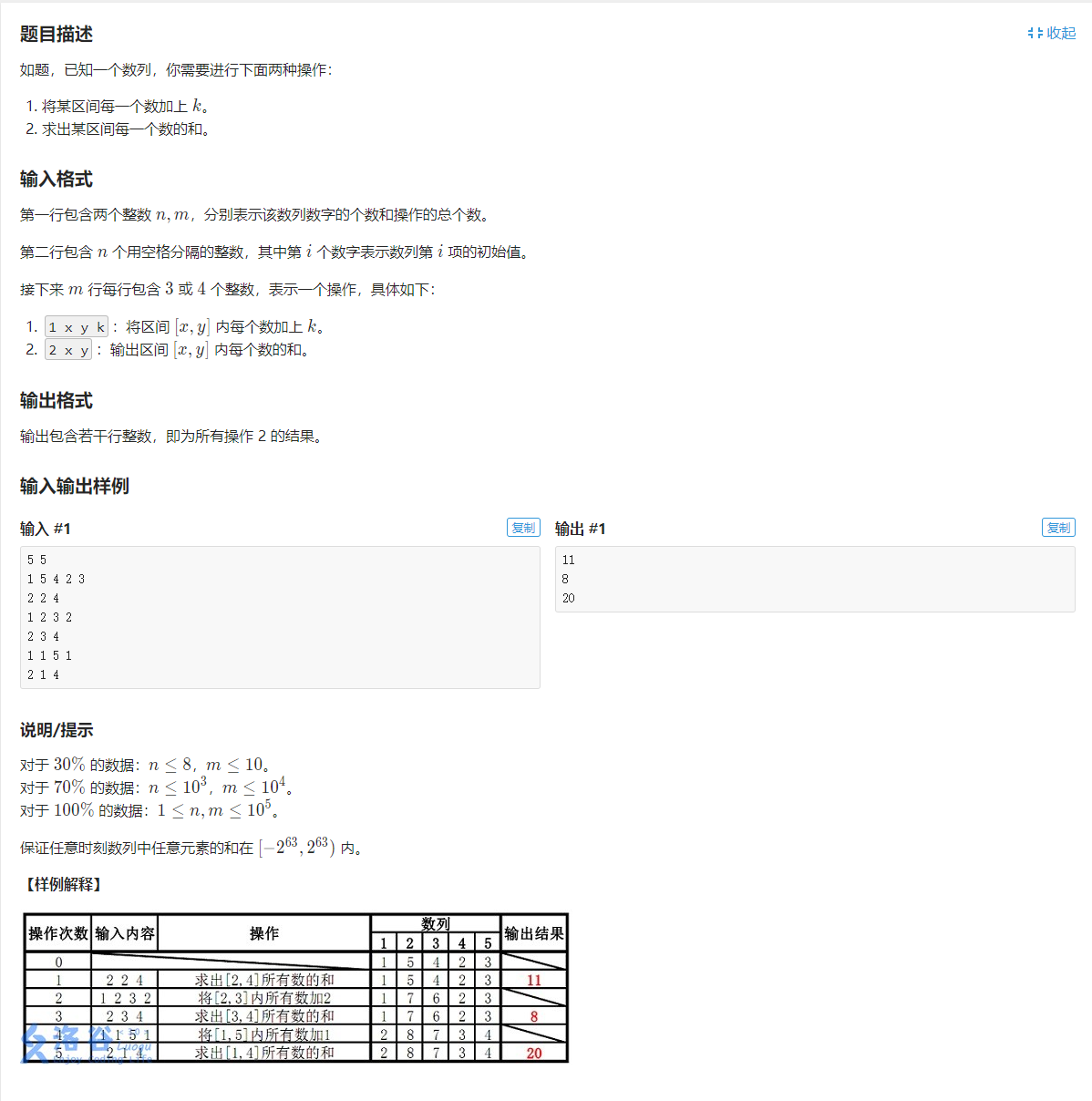
1. 单点修改，区间查询（比较特殊，最小值：（只能查找左端点在1或者右端点在n的），和：无限制）
2. 区间修改，单点查询（基础差分技巧）
   保存差分数组，利用差分技巧加减区间，单点查询就是查前缀和。
3. 区间修改，区间查询（高级差分技巧）
   维护两个数组，一个$tree1$保存$tree[i]\times (i-1)$，一个正常保存差分。
   答案就是：$(y \times ask(tree,y)-(x-1)\times ask(tree,x-1))-(ask(tree1,y)-ask(tree1,x-1))$
   具体的过程建议自己手推一下，加强记忆哦！

实现:

1. lowbit

#define lowbit(n) (n&-n)

2. 单点修改

void add(int pos,int val)
{
	for(int i = pos;i <= n;i+=i&(-i))
		tr[i]+=val;
}
int ask(int *tr,int m)
{
	int ans=0;
	for(int i = m;i>0;i-=i&(-i))
		ans+=tr[i];
	return ans;
}

3. 区间

void add(int *tr,int pos,int val)
{
	for(int i = pos;i <= n;i+=i&(-i))
		tr[i]+=val;
}
void add_ran(int l,int r,int val)
{
	add(t1,l,val);
	add(t1,r+1,-val);
	add(t2,l,val*(l-1));
	add(t2,r+1,-val*r);
}
int ask(int *tr,int m)
{
	int ans=0;
	for(int i = m;i>0;i-=i&(-i))
		ans+=tr[i];
	return ans;
}
int sum(int r)
{
	return r*ask(t1,r)-ask(t2,r);
}
int get_ran(int l,int r)
{
	return sum(r)-sum(l-1);
}

这时候我们已经可以完美的解决问题了，就是：

//注意要开ll哦！
#include<iostream>
#include<algorithm>
#include<cstdio>
using namespace std;
const long long maxn = 100010;
long long n,m,t,l,r,val;//n个元素,m个询问.
long long a,b;
long long t1[maxn],t2[maxn];
void add(long long *tr,long long pos,long long val)
{
	for(long long i = pos;i <= n;i+=i&(-i))
		tr[i]+=val;
}
void add_ran(long long l,long long r,long long val)
{
	add(t1,l,val);
	add(t1,r+1,-val);
	add(t2,l,val*(l-1));
	add(t2,r+1,-val*r);
}
long long ask(long long *tr,long long m)
{
	long long ans=0;
	for(long long i = m;i>0;i-=i&(-i))
		ans+=tr[i];
	return ans;
}
long long sum(long long r)
{
	return r*ask(t1,r)-ask(t2,r);
}
long long get_ran(long long l,long long r)
{
	return sum(r)-sum(l-1);
}
int main(void)
{
	scanf("%lld%lld",&n,&m);
	for(long long i=1;i<=n;i++)
	{
		scanf("%lld",&a);
		b=a-b;//差分.
		add(t1,i,b);
		add(t2,i,b*(i-1));
		b=a;
	}
	for(long long i=1;i<=m;i++)
	{
		scanf("%lld",&t);
		if(t == 1)
		{
			scanf("%lld%lld%lld",&l,&r,&val);
			add_ran(l,r,val);
		}
		else
		{
			scanf("%lld%lld",&l,&r);
			printf("%lld\n",get_ran(l,r));
		}
	}
	return 0;
}